Two ancient books, coming down the ages from over two millennia ago, are generally credited as the most well-read books of all time. The first book, the Bible (composed of the older Jewish testament and the newer Christian testament)—claimed by its adherents to be the “word of the one true God”—was written by a multitude of scribes between the late second millennium BCE and early first millennium CE. The second book is Euclid’s Elements (actually a compendium of thirteen books) written by a single author, the Greek mathematician Eucledes (better known as Euclid) of Alexandria, around 300 BCE.
The reasons both of these books are so popular are obvious. The Bible, which has been translated into every major language on Earth, is read by billions of followers of Judaism and Christianity. At the same time, Euclid’s Elements (typically the first six books) are an essential part of the math curriculum of middle and high school students around the globe.
Despite their antiquity and lasting popularity, no two books could be more unalike. While the Bible tells us what to believe unquestioningly, Euclid’s Elements shows us how to think critically.
In this essay, my focus will be on the art of thinking, defined and pursued by Euclid with clarity and vigor in his Elements, and the monumental impact that it has had not only on mathematics and science but on numerous other areas of inquiry as well.
Regarding Euclid’s life and times, much more is known about the latter than about the former.
Euclid lived in the middle of the period of human history that saw a remarkable awakening of the human intellect (starting around 600 BCE and ending around 300 CE).1 The epicenter of this intellectual awakening was Greece (which encompassed not only today’s Greek mainland and islands, but also parts of present-day Turkey, Egypt, Italy, Sicily, and Cyprus). What characterizes this period was the bold rejection of long-entrenched supernatural myths and their replacement by natural theories to explain observed phenomena. For instance, Greek thinkers posited that thunder and lightning did not happen due to the wrath of supernatural gods as was commonly believed at the time but rather due to natural processes taking place in storm clouds. Likewise, they rejected the long-prevailing view that diseases of the human body and mind were punishments from gods for whatever transgressions the victims may have committed, and they espoused the view that they arose from the natural biological malfunctions of the human body.
The Greek thinkers also began to contemplate more esoteric questions, such as the nature of matter (Democritus, circa 410 BCE), leading to atomism and the nature of motion, leading to the important questions of the divisibility of space and time as illustrated by the celebrated Paradox of Zeno (circa 445 BCE), concerning the counterintuitive result of a handicapped race between a hare and a tortoise.
Another monumental contribution to human thought by the Greek thinkers of this period was that they were the first in history to ask the question “Why?” rather than “How?” Their predecessors in many parts of the world, particularly China and Sumer, had asked the latter question “How?” and had made significant advances in technology, which simplified their daily lives, but it seems that it did not occur to them to ask the more fundamental question “Why?”
Essentially what the Greek thinkers did was to replace unquestioning mythical beliefs involving the supernatural with natural explanations (that is, theories) subject to acceptance or rejection following vigorous and unconstrained debate. This way of thinking laid the foundation for modern methods of inquiry, except that the central criterion for acceptance or rejection of a theory, at present, is observation and experimentation. Furthermore, modern scientific theories are highly mathematical, making their predictions not merely qualitative but also quantitative.
Another intellectual domain in which the Greeks of this time made seminal contributions was mathematics, particularly in the fundamental areas of number (arithmetic and algebra) and spatial shapes (geometry). This will be discussed at some length in this article. Here I wish to point out that several Greek mathematicians and philosophers of this period perceived a deep and intimate connection between mathematics and nature. This, they thought, was what produced an inherent order in nature and thereby made it comprehensible.
This view has since been espoused by several great scientists of more recent times. One was the Italian astronomer and physicist Galileo Galilei (1564–1642 CE), who is credited with starting the modern mode of scientific investigation, giving the pivotal role to observation and experimentation. He thereby demolished the entrenched anthropocentric Aristotelian cosmology (strongly embraced subsequently by the Roman Catholic Church) that had prevailed for almost two millennia. Galileo also recognized the indispensable use of mathematics in describing the cosmos and is quoted as saying, “The grand book, the universe, that is open to us all, is written in the language of mathematics.”
This view was subsequently echoed by two of the greatest scientists of all time: Isaac Newton (who had to develop an entirely new branch of mathematics, differential calculus, to describe the dynamics of the planetary system) and Albert Einstein (whose theory of relativity [both special and general] completely revolutionized the prevailing Newtonian views of space-time, matter, energy, and gravitation). Einstein’s general theory of relativity, neatly encapsulated in his so-called field equations, using the tools of higher mathematics called tensors, relates the local geometry of space-time to its material contents (matter and energy). In doing this, he showed that the gravitational attraction between material bodies did not arise from some physical force of unknown nature, as Newton had thought, but from the distortion of the space-time geometry by matter.
Let us now return to the main topic of this essay, Euclid. Compared with what is known about his times and even about many of his contemporaries, little is known about the life of Euclid. What is known for certain is that he spent the later part of his life in Alexandria during the reign of Ptolemy I (305–283 BCE). Indeed, Ptolemy I was responsible for Euclid’s relocation to Alexandria.
Following the death of Alexander the Great, one of Alexander’s generals took over a part of his empire—Egypt, with the port city of Alexandria as its capital—and proclaimed himself its ruler, Pharaoh Ptolemy I. Ptolemy was not only a successful soldier; he was also a historian and an enthusiastic student of mathematics. He wished to make Alexandria a major intellectual center and, toward this end, set about building perhaps the first state-sponsored research institute in Hellenistic Greece, the famous “Museum” and its attached Library, which was to become the greatest library of the ancient world. Ptolemy enticed noted scholars from all over Greece, including from Athens (the leading Greek intellectual center at the time), by providing them secure positions at the Museum/Library to pursue their research, teaching, and writing in an ideal interdisciplinary environment.
One of Ptolemy’s earliest, and undoubtably greatest, recruits was Euclid, who had received his early mathematical education at the famous Athenian Academy that Plato had founded in the middle of the fourth century BCE.
Ptolemy, who was clearly familiar with Euclid’s work, once asked Euclid if there were a shorter way in geometry than that presented in his Elements. He received a memorable response: “There is no royal road to Geometry.”
While Euclid would have realized the application of geometry to the solution of practical problems, he was not interested in such. His motivation for the study of geometry was that of a pure mathematician who valued it for its own sake. This attitude is exemplified in another famous retort attributed to him. It was his answer to a pupil who, at the end of his first lesson, had asked what he would gain by learning such things, whereupon Euclid called a servant and said, “Give him a coin, since he needs to make a gain by what he learns.”
Some Arab translations of Euclid’s Elements during medieval times have claimed that many Greek philosophers of the Hellenistic period used to post on the entrances to their schools the notice: “Let no one come to our school who has not learned the Elements of Euclid.” They seem to have simply replaced the word geometry, appearing in the earlier notice at the entrance to Plato’s Academy (circa 400 BCE) in Athens, by the phrase, “Elements of Euclid” and, in so doing, expressed the unique esteem in which they held his book. In fact, it is well known that since the time of mathematician and natural philosopher Archimedes of Syracuse (who lived a generation after Euclid), Euclid’s Elements has been constantly referenced and invariably used as the standard textbook on the subject.
Euclid was an outstanding mathematician who made several contributions not only to geometry but also to his other passion, number theory. He would certainly rank together with his illustrious predecessor, Pythagoras of Samos (circa 525 BCE) and his successors Archimedes of Syracuse (287–212 BCE) and Apollonius of Perga (262–190 BCE) as one of the greatest mathematicians of antiquity. But Euclid has come to occupy an especially exalted place, being often referred to, quite deservedly, as the “Father of Geometry.” This is largely due to what he achieved in his monumental work, the thirteen books (or volumes) that constitute his Elements. Firstly, it is a compendium of an impressive number of geometrical theorems (465 in all), including their proofs. These included some that were proved by him and many that were proved by others, such as the famous theorem attributed to Pythagoras. Due to the uniformly characteristic way in which the proofs were arrived at, it seems likely that the proofs provided by Euclid to various theorems were reworked by him and are different from the original ones given by their discoverers.
The book is more than a collection of theorems and their proofs. It provides the subject of geometry a thoroughly rigorous structure built on a solid foundation. He sets about his task by first providing a detailed list of definitions of the elements he needs for this mathematical structure, starting with points, lines, angles between lines, and simple plane figures, such as triangles, circles, and so on. Euclid then provides a list of axioms—self-evident general assumptions that he needs to generate his proofs, such as the whole is greater than the part and things that are equal to the same things are equal to one another. Finally, he provides several postulates (five in all), self-evident assumptions about the basic elements, points, lines, and planes. The most consequential postulate (one that we will revisit) is the Fifth Postulate, which states that given a straight line (l) and a point (p) outside l, there is one and only one straight line (in the plane defined by p and l) that can be drawn through p parallel to l.
Armed with these definitions, axioms, and postulates, Euclid sets out to prove the network of theorems (which he called propositions) in his Elements, starting with the simplest and proceeding to more complex ones, while building on what had already been proved. The monumental contributions to the development of geometry that Euclid made in his Elements have been recognized by mathematicians throughout the ages. The great mathematician and scientist Isaac Newton, who was very familiar with Euclid’s work and had used it in his own research, remarked: “It is the glory of Geometry that from so few principles it can accomplish so much.”
What Euclid accomplished in his Elements transcends mathematics and sets up a powerful new method for discovering general truths, starting with simple assumptions. This method, which has come to be known as the axiomatic method of deductive reasoning, has since been used in many other areas of intellectual endeavor, including but not limited to all branches of science. This will be discussed later. I will now return to Elements.
As mentioned earlier, Elements consists of thirteen books, not all of them confined to geometry as is often assumed. The first six are largely concerned with simple figures lying on a plane: triangles, rectangles, circles, and the like (“plane geometry”); the next four books deal with number theory; and the last three deal with the properties of solid figures: spheres, cones, cubes, and so on (solid geometry). The final book ends with the properties of the five regular polyhedra: the tetrahedron (four faces), the cube (six faces), the octahedron (eight faces), the dodecahedron (twelve faces), and the icosahedron (twenty faces), and their special relationship to the sphere. This was an area that greatly interested Plato. In fact, these five regular polyhedra are often described as the “Platonic solids,” and it is likely that they first attracted Euclid’s attention when he was studying at Plato’s Academy in Athens.
My own introduction to geometry took place when I was in middle school in Sri Lanka (circa 1948). It came from a highly abridged English translation of the first six books of Euclid’s Elements. Even as a young student, it did not take too long for me to grasp the power and beauty of Euclid’s axiomatic method of deductive reasoning, discussed earlier. This laid the foundation for my abiding interest in mathematics.
One of the methods used extensively by Euclid to establish his propositions (theorems) that made a deep impression on me was the method referred to as reductio ad absurdum. What this means is that if we start with a premise (assumption) and proceed by logical deduction to a conclusion that contradicts our premise, then our premise must necessarily be wrong (absurd).
Euclid uses this method very cleverly. Faced with having to establish a proposition (P), which is not easy to prove directly, he starts with the alternative proposition that contradicts P, call it Q. He then proceeds to a conclusion (C) that contradicts Q. So Q must be false, and therefore its opposite P must necessarily be true. An early, simple example of this strategy that I recall is the following: two circles, whose centers are A and B, touch each other externally at point C. You are required to prove the proposition (P) that the line joining A and B passes through C. This seems obvious when you inspect the figure (touching circles), but not so easy to prove directly. So Euclid assumes that P is false, that the line joining A and B does not pass through C, and easily shows that this leads to a falsehood (using a proposition established earlier, that the sum of two sides of any triangle is greater than the third), thereby establishing that P is true.
Perhaps the most celebrated proposition (Proposition 30, Book IX) that Euclid proved using this strategy was not in geometry but in number theory (which I learned much later in college). It concerns the class of numbers that are called prime numbers (primes), defined as those whole numbers (integers) that are divisible only by themselves and 1. Examples of primes are 2, 3, 5, 7, 11, 13, etc., while integers such as 4, 6, 9, 15, etc. are clearly not primes, according to the above definition. Mathematicians from very early times have been intrigued by prime numbers and have proceeded to discover larger and larger prime numbers; the largest discovered to date has more than seventeen million digits. Early on there was a debate as to whether the number of primes was finite or infinite. Euclid proved that this number was indeed infinite. Propositions involving infinity are not easy to prove directly, so Euclid uses the aforementioned reductio ad absurdum method to prove it. He starts with the proposition (P) that the number of primes is finite. In that case, there must be a largest prime number, which is represented by L. Next, he considers the number, N, which is the product of all the primes up to the largest, plus 1. In other words, N = (2 × 3 × 5 × – – – × L) + 1. It is clear that this number cannot be divided by any of the primes (within the parentheses) because of the additional 1. Thus, N is, by definition a prime. Because N is clearly larger than L, which was assumed to be the largest in the finite set of primes, the conclusion that has been reached contradicts the starting premise that there are only a finite set of prime numbers. So that premise is false. Because there are only two possibilities, the alternative premise that there are indeed an infinite number of primes is necessarily true. This established the theorem that he set out to prove. (QED or Quod Erat Demonstradum).
One of the best-known propositions in Euclid’s Elements is Proposition 47, Book I, better known as the Pythagorean Theorem (named after the mathematician who first proved it two centuries before Euclid). The theorem states that in any right-angled triangle, the square of the length (a) of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths (b, c) of the other two sides (i.e., a2 = b2 + c2). The proof provided by Euclid, which included several constructions and was a bit involved, could have been the same as that given by Pythagoras, or it might have been reworked by Euclid. Different proofs of the theorem have since been offered by other mathematicians, but remarkably the simplest and most elegant one is due to Albert Einstein, which he provided when he was just twelve years old.2
The Pythagorean theorem is a highly consequential theorem in all of geometry and is also at the heart of the algebraic form of geometry called trigonometry. Even more importantly, it resulted in the discovery of a whole new class of numbers, called irrational numbers.
To be continued in the next issue of Free Inquiry.
Notes
1 This period of intellectual awakening began about 600 BCE in the Greek empire. Among the reasons espoused for this awakening is that it was a time of increasing prosperity, which produced an elite class of intellectuals with time for contemplation. Also, the Greek polytheistic religion of the time was far from centralized, and there was no organized church or powerful clergy. This enabled unhindered free inquiry and debate on any subject that interested Greek thinkers. The period came to an end following the defeat of the Greeks by the Romans and the subsequent ascendancy of the powerful Roman Catholic Church. The Church ruthlessly suppressed free thought by persecuting its practitioners and burning their books. The single most devastating blow to free thought and scholarship took place in 391 CE, when a crazed mob of Christian fanatics burned to the ground the famed Museum and Library in Alexandria, which was the greatest repository of knowledge in the ancient world. This barbaric act was followed by another in 415 CE when Hypatia, the most prominent woman mathematician, astronomer, and philosopher of the ancient world (who was also associated with the aforementioned Library) was brutally murdered in the streets of Alexandria by another crazed mob of Christian fanatics, her only crime being that she had fearlessly continued to extol people not to accept religious claims unquestioningly.
These appalling actions were the forerunners of what has come to be known as the Dark Ages, from which the Western world would not emerge until more than a millennium later, starting with the Renaissance in the seventeenth century. The Renaissance rekindled the skepticism and naturalistic thinking of the ancient Greeks and gave us modern science. Modern science has demonstrated that the real world is indeed comprehensible and deeply interwoven with mathematics, as the ancient Greeks correctly perceived beginning twenty-six centuries ago.
We now live in an age defined by modern science and its associated advanced technology. Yet the mental virus of religious fundamentalism and its connected pathologies of fanaticism and intolerance are, sadly, not yet things of the past. It keeps reappearing after brief periods of dormancy, as is presently evidenced in numerous parts of the world, including the Middle East and United States.
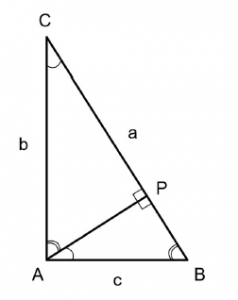
2 Following is Einstein’s proof of the Pythagorean Theorem. The right-angled triangle (ABC, figure 1) is divided into two smaller right-angled triangles (ABP) and (ACP) by drawing a perpendicular (AP) from A to the hypotenuse (AB). Inspection of the figure shows that the three right-angled triangles are similar (have corresponding angles equal). Therefore, from the proportionality property of similar triangles, it follows that:
BP/AB = AB/BC → (AB)2 = BP × BC — (1)
And PC/CA = CA/BC → (CA)2 = PC × BC — (2)
Adding (1) and (2) we get (AB)2 + (CA)2 = (BP + PC) × BC
= BC × BC = (BC)2
(QED).
In fairness to Euclid, it should be noted that Euclid systematically proved his theorems by using the results of his previously proved theorems. So, he could not use the proportionality property of similar triangles to prove Pythagoras’s theorem, because the former appears much later in Book VI (Proposition 4).



